Con la disponibilidad de capacitores con capacitancias muy grandes, los supercapacitores, es de gran importancia para el profesional de la electrónica saber cómo realizar cálculos con estos componentes. En este artículo, cubrimos algunos cálculos importantes con estos componentes.
Le recordamos que estos cálculos tienen sus fundamentos dados en nuestro libro Aprende Electrónica – Curso Básico y en varios artículos de nuestra sección Matemáticas para Electrónica. El lector también puede encontrar toda esta teoría en los libros de texto de física de la escuela secundaria.
Importancia
En las aplicaciones actuales, los supercapacitores se utilizan principalmente como fuentes de energía. Con capacidades del orden de muchos farads, pueden utilizarse como fuentes de energía en muchas aplicaciones.
Sin embargo, los supercapacitores que tenemos hoy en día son dispositivos de baja tensión, del orden de unos pocos voltios, lo que lleva a la necesidad de realizar su asociación en el momento de su uso. Asimismo, a la hora de cargar estos componentes, esta limitación requiere un cuidado especial.
Así, el lector que pretenda utilizar supercapacitores asociados como fuentes de energía debe estar preparado para saber cómo se comportan en un circuito, especialmente si tienen valores diferentes.
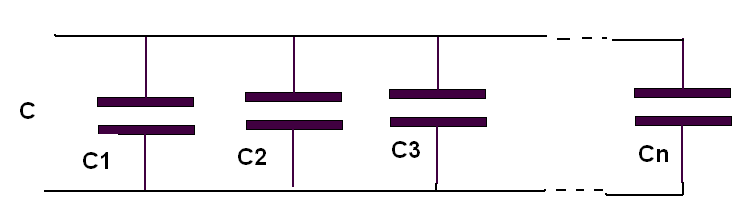
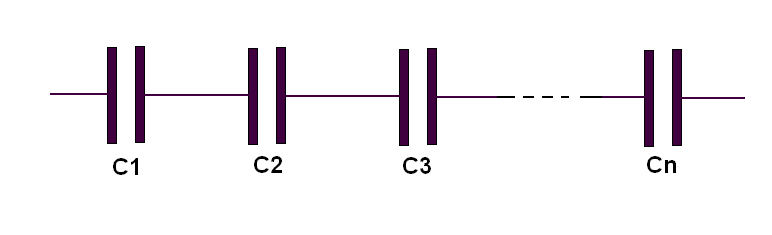
Así, damos a continuación un ejemplo de cálculo con supercapacitores, recordando que en asociación en paralelo se suman sus capacitancias, y en asociación en serie la capacitancia equivalente viene dada por la fórmula abajo:
Un cálculo práctico:
Imaginemos que el lector obtiene dos supercapacitores, uno de 30F y otro de 60F, ambos con un tensión de 3.3 V, deseando usarlos en un proyecto donde alimentarán un circuito electrónico.


Sucede que tengo la intención de cargarlos en serie en una fuente de 5V, porque ciertamente no podré conectar una cubierta directamente a la fuente, ya que los 5V son más que la tensión nominal que tienen. Entonces tenemos el siguiente circuito para la carga:
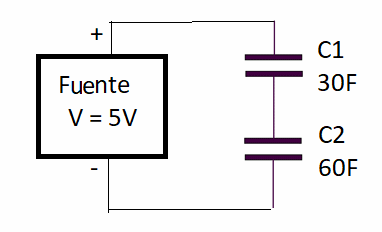
Vea que en la práctica no se recomienda la conexión directa de la fuente en los capacitores descargados, porque la corriente inicial representa un corto que puede dañar la fuente. Debe haber un circuito propio que limite la corriente inicial a un valor seguro.
Una vez cargados, conectamos los capacitores en paralelo, esperando que la tensión obtenida se acerque a los 2,5 V (la mitad de los 5 V que esperamos que sea la tensión de la carga de cada uno. ¿Es esto lo que sucede?
Empezamos entonces calculando la resistencia equivalente que obtenemos cuando conectamos los dos capacitores en serie, en el proceso de carga:
1/C = 1/30 + 1/60
O:
C = (C1 x C2) / (C1 + C2)
Fórmula simplificada cuando tenemos dos capacitores Obtenemos:
C = (30 x 60)/(30 + 60)
C =1800/90
C = 20F
Volviendo al circuito de carga, vemos que la carga almacenada en cada capacitor será:
Q = C x V
Q = carga en Coulombs
C = Capacitancia equivalente
V = tensión del circuito
Q = 20 x 5 = 100 Coulombs
Una propiedad importante de la asociación en serie de capacitores es que, independientemente de los valores de los capacitores asociados, todos cargan con la misma carga.
Es importante que las tensiones también sean diferentes, lo que en el caso de capacitores de diferentes valores se debe considerar, porque puede superar los 2,7 V. Con el valor de la carga, el proyector puede calcular la tensión con la que se cargó cada uno.
Sin embargo, si los conectamos en paralelo ahora, las cargas se repartirán y aparecerá una cierta tensión en la conexión en paralelo. ¿Cómo calcular el valor?
A) Tenemos la carga en cada capacitor: 100 Culombios
B) Tenemos la capacitancia equivalente en paralelo (30F + 60F)
La tensión será entonces:
V = Q/C
V = tensión
Q = carga
C = capacitancia
V = 100/90
V = 1,11 V
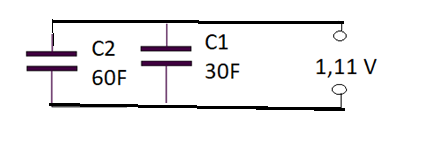
Muy diferente de lo esperado. ¿Por qué?
Está claro a partir de estos cálculos que los diferentes valores de los capacitores causaron que la distribución de carga y tensión no ocurriera de manera uniforme.
Así, cuando trabajemos con supercapacitores o incluso electrolíticos y deban estar asociados, debemos ser conscientes de esa distribución desigual de cargas y tensiones que se produce con componentes de diferente valor.
Una pequeña diferencia en el valor no afecta mucho los resultados, pero una diferencia mayor como la del ejemplo dado condujo a una tensión mucho más baja que el esperado en el banco de dos capacitores.
El mismo cuidado se debe tener en los cálculos cuando se trabaja con bancos de muchos capacitores.
Y, para los lectores que se preparan para un examen de ingreso, un concurso que requiere conocimientos sobre capacitores al nivel indicado, esta es una pregunta que se puede incluir.
Sugerencias:
a) Haga los mismos cálculos para dos supercapacitores del mismo valor.
b) ¿Existiría el peligro de que uno o más supercapacitores se quemaran con la carga por la tensión superior a 2,7 V que aparecería entre sus armaduras? Calcule
c) Proponga a sus alumnos cálculos que involucren más de dos supercapacitores.