Una comparación que hemos hecho, y que muchos otros hacen, con la aparición en el mercado de super capacitores con más de 10F es que si estuvieran preparados con tecnología convencional, serían del tamaño de la tierra. Incluso hemos recibido mensajes diciendo que esto es una exageración, y que no corresponde a la realidad. En este artículo vamos a probar que un capacitor de 1F sería no sólo el tamaño de la tierra, pero mucho más grande.
La enseñanza de la física se basa en principios muy bien establecidos a través de años de estudio. Este es el caso de la electricidad estática que aprendimos en la escuela primaria el electrificando objetos y luego en la escuela secundaria con cálculos que involucran fuerzas, campos y potenciales.
En estos estudios, un punto importante para la electrónica es lo que se ocupa de las cargas almacenadas en los cuerpos y capacitores.
Por lo tanto, aprendemos que un cuerpo puede ser electrificado, es decir, puede almacenar cargas eléctricas y que arreglos especiales de conductores e aislantes pueden aumentar esta capacidad de almacenamiento, dando lugar a componentes que ahora conocemos como capacitores.
Para que podamos matar nuestra curiosidad por los capacitores del tamaño de la tierra, partiremos de una esfera metálica. Un conductor montado en un pedestal y que se utiliza en muchos experimentos de física en la escuela secundaria, cursos técnicos e incluso superiores.
Cuando se carga esta esfera está almacenando cargas eléctricas, es decir, es un capacitor esférico.

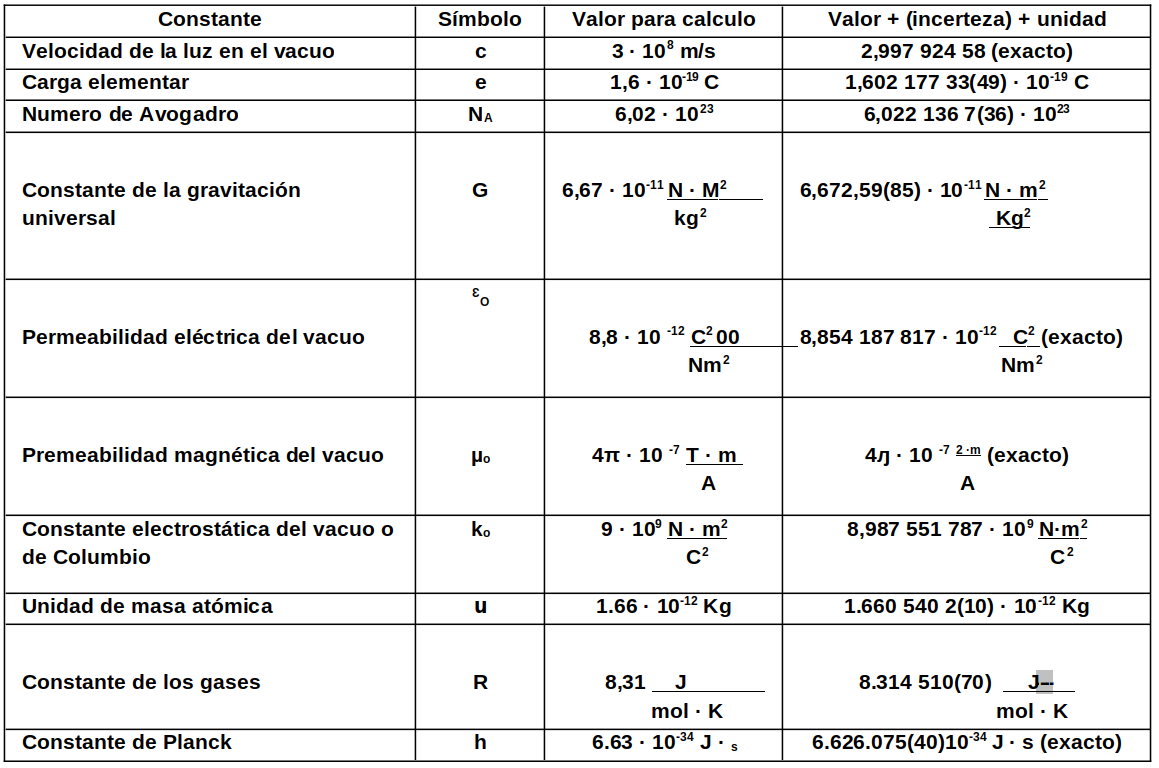
Aprendimos que un capacitor necesita tener dos armaduras, uno positivo y otro negativo, lo que llevaría a la idea de que un capacitor esférico, por ejemplo, estaría formado por dos conductores concéntricos, separados por un dieléctrico, como se muestra en la figura 2.
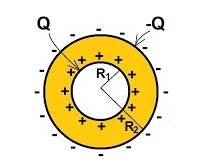
Sin embargo, también podemos considerar una sola esfera si es una de las armaduras y la otra está en el infinito. Por lo tanto, las líneas de fuerza del campo eléctrico salen radialmente de la esfera, como estamos acostumbrados a representar. La carga de esta esfera es la carga del capacitor.
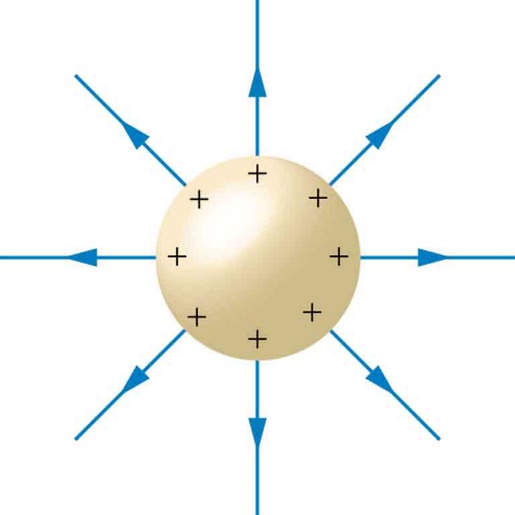
La cantidad de cargas almacenadas divididas por la tensión en la que se encuentran nos da capacitancia, por la fórmula conocida:
C = Q/V
Vemos que esta capacitancia C depende del tamaño de la esfera.
Pero en un capacitor esférico, ¿cómo podemos calcular la capacitancia dependiendo de su tamaño.
Podemos escribir una fórmula que diga cuál es la capacitancia dependiendo de la distancia entre las armaduras al centro de la esfera:
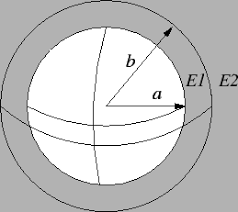
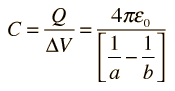
Esta fórmula, por ejemplo, puede tener en cuenta que la ionosfera es una capa de nuestra atmósfera conductora y podría utilizarse en la fórmula.
Pero podemos simplificar esta fórmula teniendo en cuenta sólo una esfera del tamaño de la tierra, es decir, un conductor esférico cargado.
Con esto, el término b de la fórmula tendría al infinito y con esto podríamos tener 1/b = 0, eliminando ese término. La fórmula sería:

De acuerdo, sabemos π vale 3.14, pero ¿qué ese extraño factor de qué se trata? Es una constante, algo muy común en las fórmulas físicas.
Cuando cuantificamos algún fenómeno a través de una fórmula, experimentamos y anotamos los resultados, utilizando unidades que establecemos. Por ejemplo, medimos distancias en metros, fuerzas en Newtons, etc.
Sin embargo, los resultados prácticos no siempre funcionan con valores que no se corresponden con la realidad que medimos. Por lo tanto, tenemos que añadir en las fórmulas el factor que las adapta a las unidades utilizadas. Este factor es un número que no cambia.
Lo que sí sabemos es que, si no usamos estas constantes, la fórmula no funciona y si usamos todo es de acuerdo con lo que observamos en la práctica.
En la tabla siguiente tenemos algunas constantes que se utilizan en los cálculos de física.
Vea que una de ellas es precisamente el εo. Es la "constante dieléctrica del vacío" asumiendo que entre la tierra y lo infinito tenemos más vacío que atmósfera.
El valor se obtuvo a través de experimentos, siendo utilizado en cualquier cálculo que involucra capacitores, por ejemplo, Su valor:
ε 8.852 x 10-12 (no nos preocupemos aquí por las unidades)
Por lo tanto, en los cálculos donde aparece esta constante, tenemos que reemplazarla con ese valor.
Entonces llegamos al punto que importa. ¿Qué capacitancia tendría una esfera metálica del tamaño de la tierra?
Vamos a adoptar un rayo aproximado de 6.000 Km a la tierra, o 6 x 106 metros.
Entonces tenemos para nuestro problema:
C = queremos calcular
Π= 3,14
A = 6 x 106
εo = 8.852 x 10-12
Poniendo en la fórmula tenemos:

C = 4 x 3,14 x 8,852 x 10-12 x 6 x 106
C = 0,67 x 10-3 F
C = 0,67 mF
Valor muy pequeño, en comparación con un super capacitor.